Règle des tiers, nombre d’or et consorts…

Patrice FOIN

Règle des tiers et nombre d’or, présentation.

Pour bien construire une photo, une règle souvent donnée aux photographes débutants est la « règle des tiers ». Elle consiste à dire qu’il ne faut surtout pas mettre le sujet principal au beau milieu de la photo, mais au contraire qu’il faut le centrer sur des lignes, horizontales et/ou verticales, situées au tiers de celle-ci. C’est ainsi qu’en suivant cette règle, la ligne d’horizon ne doit jamais être au milieu mais au tiers supérieur ou au tiers inférieur de la photo. Cette règle est très valable mais accepte comme toujours des exceptions ! Par exemple, il est des photos construites sur une symétrie parfaite et qui sont des chefs-d’œuvre. Pour diverses raisons, la ligne d’horizon peut au contraire se trouver beaucoup plus près du haut ou du bas de la photo, etc. La règle des tiers est une bonne règle… pour débuter ou lorsqu’on est perdu dans la construction de sa photo… mais il faut aussi savoir la transgresser quand c’est nécessaire... On va voir dans la suite les liens approximatifs entre cette règle et le nombre d’or.

Pour ne pas vous submerger de laïus, je reviendrai seulement à la fin sur les usages qui ont été faits du nombre d’or au cours des temps.

Le nombre d’or est un nombre qui se rencontre en mathématique dans des constructions géométriques simples et aussi dans des calculs simples dont certains font intervenir la racine carrée du nombre 5. Il peut servir à la construction des photos et à bien d’autres choses… Sa valeur approchée est de :

Ou encore :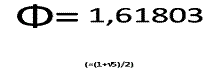

Une première construction à partir du nombre d’or.

A partir de ce nombre, commençons à faire des constructions qui peuvent nous servir. Tout d’abord, on peut construire un rectangle qui soit dans cette proportion et qu’on appelle rectangle d’or, voire rectangle doré. Il est ci-dessous en noir parmi les autres formats courants (format A4 : format des papiers courants, format 20x30 : format dans le même rapport que beaucoup de capteurs de vos boîtiers, format 16/9 : format le plus courant pour les téléviseurs et aussi les écrans des ordinateurs.

Une première utilisation du nombre d’or en photo peut être de recadrer la photo dans ce rapport. Ça n’est pas le plus intéressant mais c’est déjà quelque chose !

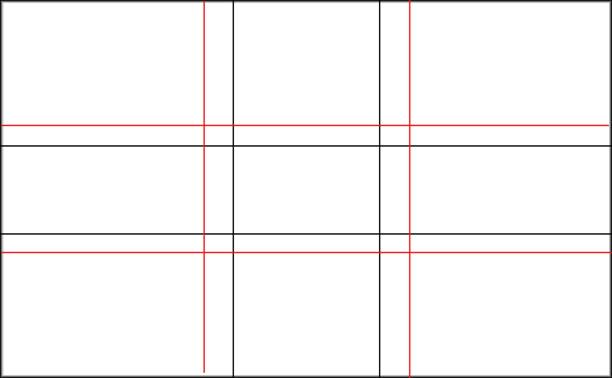
Quel que soit le format de la photo recadrée ou non, il est possible de s’appuyer sur un découpage fondé sur le nombre d’or. A partir de l’exemple ci-dessous, on peut par exemple s’arranger pour mettre une horizontale majeure de la photo (ligne d’horizon par exemple) sur l’une des lignes horizontales, ou encore une verticale majeure (tronc d’arbre, etc.) suivant une des lignes verticales

Comparons avec la règle des tiers. Le découpage suivant le nombre d’or (ou « découpage doré ») est en noir, celui suivant la règle des tiers en rouge. :

Exemple de ce type de construction suivant le nombre d’or (ou à peu près…) sur une photo puis construction avec la règle des tiers sur la même photo. Ensuite, comparaison des deux.

En haut, cadrage suivant le nombre d’or, en bas suivant la règle des tiers.

Et si vous aussi, vous voulez vous amuser à ce genre de construction, voici le calque qu’il vous faut en cliquant ci-dessous :

Calque nombre d’or / règle des tiers

De plus en plus fort ! Le nombre d’or, la spirale logarithmique et la photo…

Une des manières d’appréhender géométriquement le nombre d’or est de dire que si l’on prend un « rectangle doré » et qu’on construit dedans un carré, le rectangle « qui reste » est encore un rectangle doré qui a la même propriété. On peut ainsi continuer « à l’infini ». Comme un petit croquis vaut mieux qu’un long discours, exemple ci-dessous :

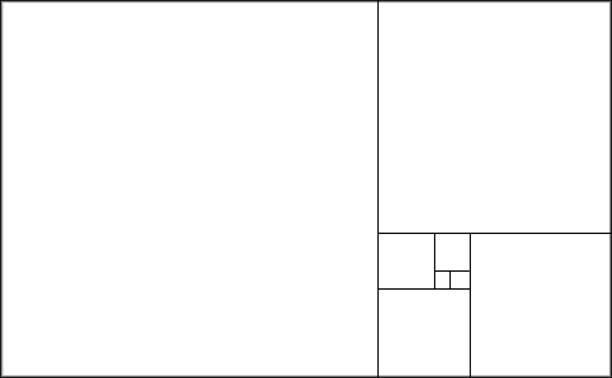
Et, encore plus fort… si l’on inscrit un quart de cercle dans chacun des carrés de plus en petit, on obtient la figure ci-dessous :

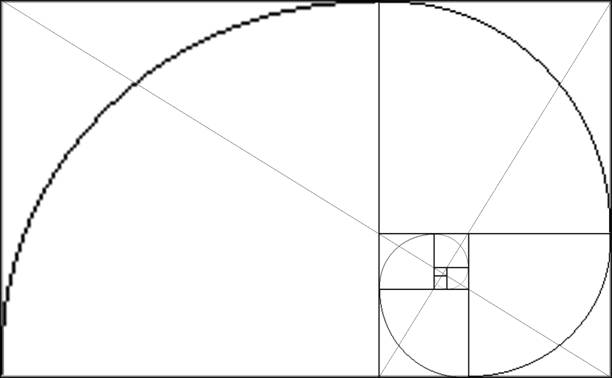
Si cette belle spirale n’est pas très exactement, au sens mathématique du terme, une spirale logarithmique, elle s’en rapproche énormément. Elle peut servir de base à des constructions très intéressantes.

Tout d’abord, quelques remarques à ce sujet :

-il y a quatre possibilités de construction suivant le sens dans lequel on part ;

-si le rectangle qui délimite la photo n’est pas un « rectangle doré » mais dans les proportions du A4 ou de 2000x3000, on peut très bien faire une homothétie pour inscrire la spirale juste dans le rectangle que l’on traite (en général, fonction « homothétie » dans les logiciels de traitement d’images les plus courants) ; c’est mieux que rien !

-un point intéressant est le « centre de la spirale » (le point vers lequel elle converge quand on continue la construction à l’infini) ; suivant le sens dans lequel on construit la spirale, il y en a quatre sur la photo ; l’œil semble assez naturellement attiré vers ces points et l’on peut donc avoir fortement intérêt à mettre en correspondance avec l’un d’eux le cœur du sujet que l’on traite, ce vers quoi l’on veut que l’œil du spectateur soit attiré ; bien évidemment, si l’on a une grosse tache blanche qui se balade n’importe où ailleurs sur la photo, l’œil pourra être tout d’abord attiré par elle et l’effet sera raté… ne m’en rendez pas responsable !

Et maintenant, un exemple pratique. En fait, je dois avouer que c’est parce que je trouvais la construction de la photo qui va suivre intéressante que je lui ai appliqué la construction en question et non l’inverse :

En superposant une première spirale, on obtient :

On voit tout de suite que le nombre d’or se trouve un peu partout dans cette photo : côté gauche et dans une moindre mesure côté droit de la tour, niveau de la berge en face, ligne générale des arbres à gauche, qui suit globalement la spirale, etc. Par contre, le centre de la spirale ne correspond à rien, pas plus dans le montage suivant, mais on ne peut pas tout avoir à la fois :

Sur ce dernier montage, la « construction dorée » apparaît pour toute la partie en bas à gauche : niveau de l’eau, limite des remparts, berge qui suit la spirale.

On notera que pour matérialiser le point de convergence de la spirale, il suffit de prendre l’intersection des diagonales des deux plus grands rectangles dorés, ce que j’ai tracé sur le calque.

Maintenant, si vous voulez en faire autant : voici un lien avec une des versions de ma spirale. A vous de lui faire subir les mises à l’échelle et les symétries que vous souhaitez.

Spirale logarithmique

Et pour ceux qui le souhaiteraient, une petite séquence d’instructions dans un Photoshop très ancien mais qui devrait leur permettre de la superposer à leurs photos :

-ouvrir la photo sur laquelle vous voulez travailler

-ouvrir le fichier anombedor1

-cliquer à droite et faire "tout sélectionner" dans celui-ci

-faire édition/copier

-aller dans la photo

-faire édition/coller

-faire fenêtre/afficher les calques (s'ils ne sont pas déjà affichés)

-mettre en mode "produit" avec "opacité à 100%

-la spirale et la construction doivent alors être en superposition à la photo, les ajuster à la photo ou à la zone de la photo intéressante par:

-édition/transform/homothétie

-ajuster en jouant sur les côtés du calque contenant la spirale et la construction

-quand c'est fait, "entrée" ou "enter" suivant la langue que parle votre clavier...

et voilà le travail!

Si vous voulez mettre la spirale et la construction dans un autre sens par rapport à la photo:

-édition/transform/symétrie (à axe vertical ou horizontal suivant votre choix) puis "entrée" ou "enter"

Quelques autres constructions s’appuyant sur le nombre d’or :

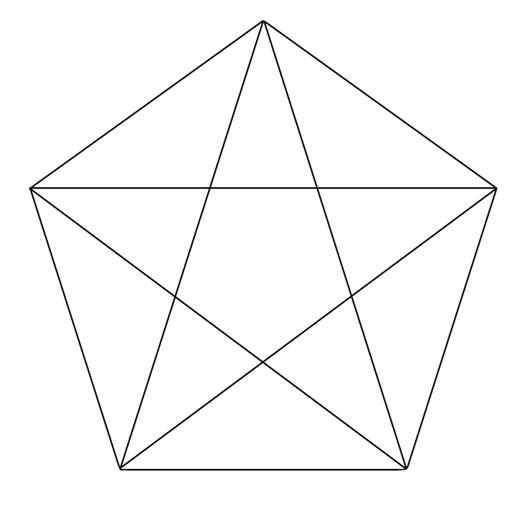
Le grand classique est le pentagone régulier, qui contient le nombre d’or un peu partout. Il est censé avoir servi à de nombres peintres dont Léonard de Vinci. Faites-en bon usage ! Personnellement, je ne l’ai pas encore utilisé….

Et puis un rectangle bien aplati :

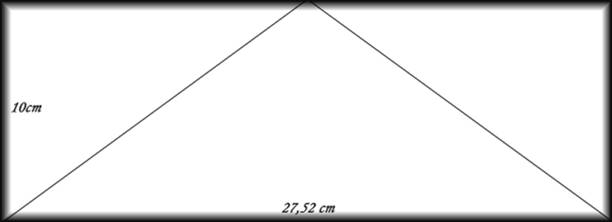
Pour les amateurs de panoramique, il pourrait constituer un format intéressant ! Le nombre d’or se retrouve dans les triangles.

Et maintenant, quelques éléments pour ceux qui veulent en savoir plus.

Quand on s’intéresse un peu à la peinture des siècles passés, on s’entend souvent dire que tel tableau est entièrement construit à partir d’une géométrie liée au « nombre d’or ». Un Léonard de Vinci est censé avoir (sur)exploité ce mode de construction… Il en va de même pour l’architecture. Les pyramides d’Egypte, parmi bien d’autres, font les régals des « chasseurs de nombre d’or »… tout comme ceux des ésotéristes, des chasseurs de trésors et de toute sorte de gens qui recherchent le mystère partout…

Les éléments simples que j’ai mis précédemment sont juste à l’usage des photographes n’ayant pas de connaissances mathématiques particulières.

Je pourrais faire de nombreux développements sur la mathématique du nombre d’or, les suites de Fibonacci, la géométrie du pentagone, etc. Je ne les ferai pas car ils se trouvent sur Internet sans problème, avec des développements sans doute mieux bâtis que ce que je pourrais faire ici. En outre ça n’est pas mon sujet.

Le nombre d’or dans la « littérature ».

Si vous consultez en détail des documents sur les constructions de l'art classique, vous verrez que celles-ci ne sont pas toujours fondées sur le nombre d'or mais aussi sur les perspectives ou d'autres choses ou une combinaison de plusieurs choses (parfois même, contrairement à tout ce qu'on enseigne aux photographes débutants, sur la coupure en deux parties égales en hauteur ou largeur, ou encore carrément la symétrie..., parfois aussi sur un découpage de l'œuvre en deux suivant la diagonale ; il semblerait que Bruegel l'ancien ait été assez friand de cette dernière...). Dans la période récente, les constructions d'un Escher ou d'un Chirico sont passionnantes (pour qui aime...) mais hélas guère transposables en photo sauf montage complètement fantaisiste car certaines perspectives "se croisent les bras" volontairement. Il y a donc beaucoup à dire sur la construction. Mais ça a déjà été fait par bien plus compétent que moi et je m’en suis donc tenu au B-A BA du nombre d’or en photo.

Sur la construction en général, on pourra consulter avantageusement :

http://expositions.bnf.fr/fouquet/arret/geometrie

et d'une manière plus générale:

http://classes.bnf.fr/fouquet/

Ci-dessous, un exemple dans lequel le point de convergence de la spirale a été utilisé conjointement à une construction suivant la diagonale :

Pour tenter de me clarifier les idées, à titre personnel comme pour écrire ceci, j’ai pris un certain nombre de documents (livres ou sites Internet) concernant le nombre d’or. J’ai parfois eu la fâcheuse impression de nager dans la folie ! Il est fréquent que leurs auteurs voient et prétendent trouver le nombre d’or partout ! Cela semble parfois tourner à la superstition ou être lié à un ésotérisme que je trouve personnellement de très mauvais goût… Le mot « numérologie » vient à l’esprit…

Les auteurs en question voient le nombre d’or non pas seulement dans les œuvres humaines mais partout dans la nature. Il est juste de dire qu’il y est bien présent... dans certains cas… mais de là à vouloir faire « rentrer au chausse-pied » tous les éléments de la nature « dans » le nombre d’or, il ne faut pas exagérer ! Par exemple, une simple réflexion géométrique montre qu’un nautile (ou une ammonite dans le passé) qui « veut » croître en spirale aura tendance à croître suivant la spirale logarithmique liée au nombre d’or… (ou « spirale d’or »). Il n’y a rien de « magique » là-dedans ! Tout au plus un peu de physique et de géométrie de bas niveau… Mais « aura tendance » seulement, car uniquement si d’autres phénomènes n’interagissent pas pour tout changer. J’ai à l’esprit ces coquilles d’ammonites qui, après avoir cru en spirale, se sont mises à décroître et se resserrer à la fin de leur vie pour d’obscures raisons (sénescence ?) qui mettent en pièce leur début de construction lié au nombre d’or…

Le nautile fossile ci-dessous (coenoceras sp.) décrit une superbe spirale logarithmique naturelle !

Il n’en va pas de même pour l’ammonite ci-dessous (stephanoceras sp., bajocien). En effet, sur la fin de sa vie (!), elle a eu le mauvais goût d’arrêter de faire croître la dimension de sa coquille, si bien que la belle spirale amorcée n’a pas été poursuivie…

De même, les spirales des galaxies sont en principe (je n’ai pas vérifié…) des spirales logarithmiques. On en trouve aussi dans certaines fleurs. Par exemple, ci-dessous, une « tribu » de spirales logarithmiques qui ne manquent pas de piquant !

De toute façon, il faut être bien conscient qu’au niveau géométrique, il est tentant d’utiliser les racines carrées des premiers nombres premiers : 2, 3, 5, d’autant plus qu’elles conduisent à des constructions géométriques très simples (et plus compliquées si l’on veut pousser ensuite les choses). Le nombre d’or est lié à la racine carrée de 5 qui se prête à des constructions géométriques très variées. Pour ne prendre qu’un exemple différent, nous utilisons tous quotidiennement une construction fondée sur la racine carrée de 2 sans même en être conscient. Il s’agit du format A4 et de tous les formats liés : A5 ou A3, A2, etc. Personne ne voit rien de surnaturel là-dedans, c’est juste bien pratique ! De même, racine de 2 se trouve dans le carré… mais qui s’amuserait à dire qu’il a construit sa photo à partir de racine de 2 parce qu’il l’a recadrée en carré ? Quant à la racine de 3, elle est présente dans le triangle équilatéral, dans l’hexagone régulier ou étoilé, etc.

En conclusion je considère que le nombre d’or peut nous aider en photo, qu’il est aussi présent dans un certain nombre d’œuvres humaines ou de phénomènes naturels, mais que de là à en induire je ne sais quelle superstition, il y a un ravin qu’il ne faut pas franchir, en tout cas, que je ne franchis pas personnellement… Les Egyptiens et les Grecs anciens n’étaient pas plus bêtes que nous et souvent passionnés de géométrie, ils connaissaient le carré, l’hexagone, le pentagone et bien d’autres choses. Ils s’en sont servi pour leurs œuvres quand ils le jugeaient nécessaire, peut-être ont-ils même eu des buts magiques… mais que je sache, ils n’ont pas révolutionné le globe grâce à cela… Par contre, il me semble indéniable que certaines constructions fondées sur le nombre d’or nous donnent une impression d’harmonie. Contentons-nous de cette impression et utilisons-la donc… ou non… suivant notre humeur…